الانحراف المعياري فى التداول … كيف يمكنك حسابه؟

استخدم مصطلح الانحراف المعياري للتعبير عن نسب التباين في توزيع الوسط الحسابي لمجموعة البيانات الإحصائية سنة 1994 . و كان عالم الاحصاء الشهير كارل بيرسون هو أول من استخدم مصطلح الانحراف المعياري في العمليات الاحصائية ويعد بديلا لمصطلح إنحراف المتوسط الحسابي.

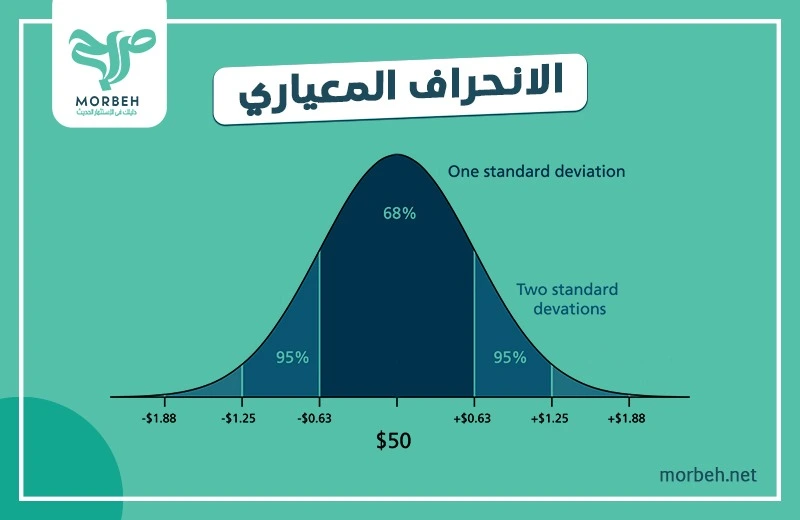
ويصف الانحراف المعيارى كيفية تشتت مجموعة من البيانات. يقارن كل نقطة بيانات بمتوسط جميع نقاط البيانات. ويعيد الانحراف المعيارى قيمة محسوبة توضح ما إذا كانت نقاط البيانات قريبة أو منتشرة. في التوزيع العادي، يخبرك الانحراف المعيارى بمدى بُعد القيم عن المتوسط ،وسوف يوضح هذا المقال كل ما يخص الانحراف المعيارى..

ما هو الانحراف المعياري؟

كان عالم الاحصاء الشهير كارل بيرسون Karl Pearson هو أول من استخدم مصطلح الانحراف المعياري في العمليات الاحصائية ويعد بديلا لمصطلح إنحراف المتوسط الحسابي.

يتم حساب الانحراف المعياري باعتباره الجذر التربيعي للتباين عن طريق تحديد انحراف كل نقطة بيانات بالنسبة إلى المتوسط. إذا كانت نقاط البيانات بعيدة عن المتوسط، فهناك انحراف أعلى داخل مجموعة البيانات. وبالتالي، كلما زاد انتشار البيانات زاد الانحراف المعيارى.

والتباين هو معدل مربعات انحرافات العلامات في التوزيع عن الوسط الحسابي. ويكون الانحراف المعيارى عندها الجذر التربيعي للتباين بالنسبة لمجموعة البيانات الإحصائية.

الانحراف المعياري والتباين:

يُشتق التباين بأخذ متوسط نقاط البيانات، وطرح المتوسط من كل نقطة بيانات على حدة، وتربيع كل نتيجة من هذه النتائج، ثم أخذ متوسط آخر لهذه المربعات.
بينما،الانحراف المعيارى هو الجذر التربيعي للتباين. يساعد التباين في تحديد حجم انتشار البيانات عند مقارنته بالقيمة المتوسطة. مع زيادة التباين، يحدث المزيد من التباين في قيم البيانات، وقد تكون هناك فجوة أكبر بين قيمة بيانات وأخرى.

قانون الانحراف المعيارى:

يتم حساب الانحراف المعيارى بأخذ الجذر التربيعي لقيمة مشتقة من مقارنة نقاط البيانات بالمتوسط الجماعي لمجتمع ما. الصيغة هي:

σ = 1 N ∑ i = 1 N ( x i − x ¯ ) 2

حيث أن:

Xi : القيمة الابتدائية في مجموعة البيانات.
X : المتوسط الحسابي.
n : عدد نقاط البيانات في مجموعة البيانات.

مثال لحساب الانحراف المعيارى:

1: احسب الوسط الحسابي للرقمين (6+10)/2 = 8 ، اذا الوسط الحسابي للبيانات الإحصائية هي 8 .

2 : احسب الانحراف الرقمي للرقمين ويمكن حسابه كالآتي

6-8 = -2 وهو مقدار الإنحراف السالب ، 10-8 = 2 ويمثل مقدار الانحراف المعيارى الموجب .

3 : قم بتربيع الرقمين الناتج من حساب مقدار الانحراف كالاتي (2) تربيع ، (-2) تربيع ليكون الناتج في كليهما 4 .

4 : قم بجمع الناتج من عملية التربيع ليصبح 4+4 = 8 .

5 : إيجاد الجذر التربيعي الموجب من ناتج عملية التربية = جذر 8 وهو 2 .

اذا الانحراف المعياري للعملية الحسابية الأولى هو الرقم 2 .

يتضح من ذلك أن الانحراف المعيارى هو ناتج جميع العمليات الحسابية من الجمع والطرح والتربيع الأرقام المعطاة في المعادلة الأولى من البيانات الإحصائية المشتتة.

خصائص الانحراف المعياري:

إن قيمة الانحراف المعياري موجبة ولا يمكن أن تكون سالبة.
علاوة على ذلك أنه يساعد في توضيح مقدار التشتت أو التباين الذي يتواجد في القيمة المتوسطة.
من الممكن أن تؤثر على أي قيم متطرفة أو قيم متطرفة في مجموعة البيانات على القيمة.
كذلك يتم استخدامه من أجل قياس التشتت أو الانتشار حول متوسط مجموعة البيانات.
كما أنه يتم استخدامه بالاقتران مع المتوسط، وذلك كي يتم حساب فترات البيانات عند تحليل البيانات الموزعة بشكل طبيعي.

مزايا الانحراف المعياري:

الانحراف المعياري هو مقياس شائع الاستخدام للتشتت. ربما يكون العديد من المحللين أكثر دراية بالانحراف المعياري مقارنة بالحسابات الإحصائية الأخرى لانحراف البيانات. لهذا السبب ، غالبًا ما يستخدم الانحراف المعياري في مجموعة متنوعة من المواقف من الاستثمار إلى الاكتواريين.

الانحراف المعياري شامل الملاحظات. يتم تضمين كل نقطة بيانات في التحليل. القياسات الأخرى للانحراف مثل النطاق تقيس فقط النقاط الأكثر تشتتًا دون مراعاة النقاط الموجودة بينهما. لذلك، غالبًا ما يُعتبر الانحراف المعياري قياسًا أكثر قوة ودقة مقارنة بالملاحظات الأخرى.

يمكن دمج الانحراف المعياري لمجموعتين من البيانات باستخدام صيغة انحراف معياري مشتركة محددة. لا توجد صيغ مماثلة لقياسات مراقبة التشتت الأخرى في الإحصاء. بالإضافة إلى ذلك، يمكن استخدام الانحراف المعياري في حسابات جبرية أخرى على عكس وسائل المراقبة الأخرى.

الانحراف المعياري مهم لأنه يمكن أن يساعد المستخدمين في تقييم المخاطر. ضع في اعتبارك خيارًا استثماريًا بمتوسط عائد سنوي يبلغ 10٪ سنويًا. ومع ذلك، تم اشتقاق هذا المتوسط من عوائد السنوات الثلاث الماضية بنسبة 50٪ و -15٪ و -5٪. من خلال حساب الانحراف المعياري وفهم الاحتمالية المنخفضة لمعدل 10٪ في الواقع في أي عام معين، فأنت أفضل مسلحًا لاتخاذ قرارات مستنيرة والتعرف على المخاطر الأساسية.

استخدامات الانحراف المعيارى:

يعتبر أداة مفيدة بشكل خاص في استراتيجيات الاستثمار والتداول حيث يساعد في قياس تقلبات السوق والأمن، والتنبؤ باتجاهات الأداء.

من المتوقع أن يكون لصناديق النمو القوية إنحراف معياري مرتفع عن مؤشرات الأسهم النسبية، حيث يقوم مديرو محافظهم بمراهنات قوية لتوليد عوائد أعلى من المتوسط.

ليس بالضرورة أن يكون الانحراف المعياري الأقل هو الأفضل. كل هذا يتوقف على الاستثمارات واستعداد المستثمر لتحمل المخاطر. عند التعامل مع مقدار الانحراف في محافظهم الاستثمارية، يجب على المستثمرين مراعاة مدى تحملهم للتقلبات وأهدافهم الاستثمارية العامة.

الانحراف المعيارى هو أحد مقاييس المخاطر الأساسية الرئيسية التي يستخدمها المحللون ومديرو المحافظ والمستشارون. تبلغ شركات الاستثمار عن الانحراف المعياري لصناديقها المشتركة وغيرها من المنتجات.

يظهر التشتت الكبير مدى انحراف العائد على الصندوق عن العائدات العادية المتوقعة. نظرًا لسهولة فهمها، يتم الإبلاغ عن هذه الإحصائية بانتظام للعملاء النهائيين والمستثمرين.

أما عن سلبياته:

لا يقيس الانحراف المعياري في الواقع مدى بُعد نقطة البيانات عن المتوسط. بدلاً من ذلك، يقارن مربع الاختلافات، وهو اختلاف دقيق ولكنه ملحوظ من التشتت الفعلي عن المتوسط.

القيم المتطرفة لها تأثير أكبر على الانحراف المعيارى. هذا صحيح بشكل خاص بالنظر إلى أن الاختلاف عن المتوسط مربّع، مما ينتج عنه كمية أكبر مقارنة بنقاط البيانات الأخرى.

ما هو التشتت؟ وما هي مقاييس التشتت؟

أن التشتت لمجموعة من القيم أو المفردات المقصود منها هو التباعد أو الاختلاف بين هذه القيم فيما بينها. عندما تكون الفروق كبيرة بين القيم ، يكون التشتت قليلا. وبناء علي ذلك من الممكن اعتبار ان التشتت القيم مقياس مقايس لدرجة تركز القيم ودرجة التقارب من بعضها البعض ، او درجة تباعدها من بعضها البعض ، وان مقاييس التشتت كثيرة ، وتختف عن بعضها من حيث الدرجة وكيفية حسابها ، وأبرز مقاييس التشتت في الاحصاء.

يوجد أربع مقاييس للتشتت ،وهما:

1- المدي: ويعرف المدي بأنه الفرق بين أكبر قيمة واصغر قيمة للبيانات ويبين الحدود التي بداخل هذه البيانات يمكن أن تقع اي قيمة

2- الانحراف المتوسط : يعرف الانحراف المتوسط لمجموعة من المفردات ، بأنه متوسط الانحرافات عن قيمة متوسطة ، مع اهمال الاشارة ، او يمكن القول بأنه متوسط الانحرافات المطلقة عن قيمة متوسطة ، ومن الممكن أن يكون الانحراف مأخوذا عن الوسط الحسابي ، فعندما يحث ذلك يمكن حساب القيم عن الوسط ، وممكن ان يكون الانحراف مأخوذا عن الوسيط الحسابي ، فيحسب انحراف القيم عن الوسيط ، والمياس الاكثر شيوعا هو انحراف القيم عن الوسط الحسابي ويكون مجموع هذه الانحرافات .

3- الانحراف الربيعي : يعرف على أنه أحد مقاييس التشتت ويعتمد علي استخدام الأقل والاعلى ويمكننا حسابه بقسمتهم علي 2 ، او كما يعرف بأن الانحراف الربيعي هو نصف المدي الربيعي

4- الانحراف المعيارى : هو الجذر التربيعي لمتوسط مربعات انحرافات القيم عن وسطها الحسابي ويعتبر هو اهم مقاييس التشتت ، وادقها وأكثرها انتشارا في التحليل الاحصائي مدى التبعثر الإحصائي، أي أنه يدل على مدى امتداد مجالات القيم ضمن مجموعة البيانات الإحصائية.